At the end of last year, we talked about the graph processing system Apache Giraph and our work to make it run at Facebook’s massive scale. Today, we’d like to present one of the use cases in which Giraph enabled computations that were previously difficult to process without incurring high latency.
The situation
Facebook’s architecture relies on various services that answer queries about people and their friends. Because of the size of the dataset, number of queries per second, and latency requirements, many of these systems cannot run on a single machine. Instead, people and their metadata are sharded across several machines. In such a distributed environment, answering queries might require communication among all these servers.
Imagine that one of our services requires fetching information about all the friends of a specific person. Such a query would be first directed to the shard that contains the person’s data (including the list of friends). Then, for each friend, a query would be issued to the respective shard, asking for the required information (see Figure 1). All the responses would then be aggregated to form the final answer.
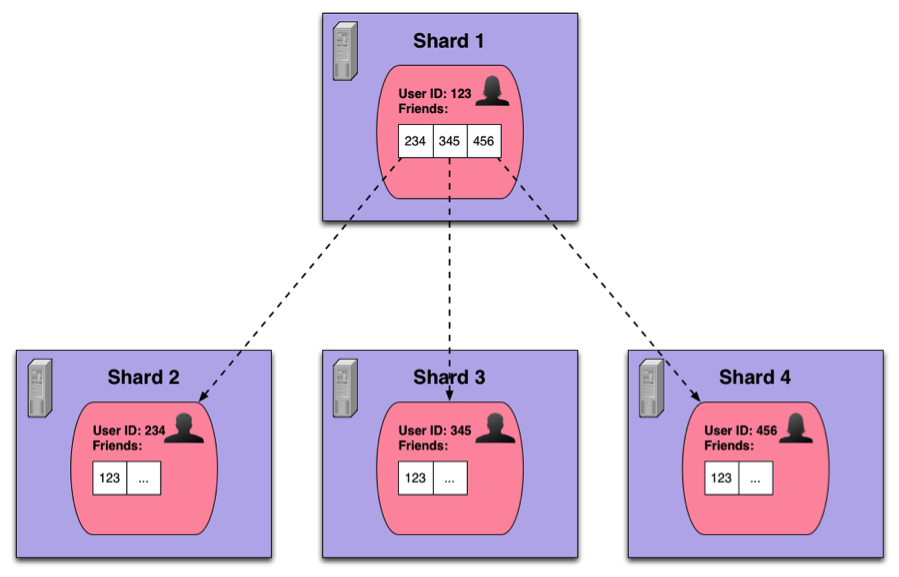
Figure 1: A query for friend data in a sharded service
If people are distributed randomly across shards (for example, by hashing their user IDs), such a query may hit almost all the machines in the system and require a lot of network traffic, which could result in high latency.
We have solved this problem by using graph partitioning, which can be formalized as follows: Given an undirected graph G = (V, E) and a natural number k, we want to partition the vertex set V into k equal-sized subsets, so as to maximize the number of edges that have both endpoints in the same partition (we call those “local edges”).
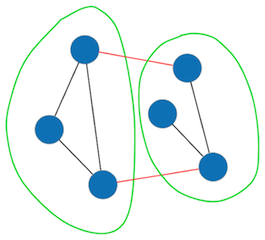
Figure 2: A graph with two partitions, with non-local edges highlighted in red
The balance constraint here is important: If too many people are allocated to the same machine, it will become a bottleneck, trumping savings in network I/O. Further, the machine may not be able to store all the data necessary (this is true for in-memory systems like Giraph). This requirement is what makes it prohibitive to compute an optimal solution for large graphs – even a simplified version with two partitions (the “minimum bisection problem”) can be proven to be NP-hard. Approximate algorithms exist, but they haven’t been proven on massive, real-world graphs yet. Hence we were looking for a heuristic that worked at our scale while still providing high edge locality.
Our solution
The high-level strategy behind our algorithm is not new: start with an initial balanced partitioning, and then iteratively swap pairs of vertices in a way that increases local edges (see Kernighan–Lin_algorithm).
We borrowed some key ideas from an algorithm previously developed at Facebook by Lars Backstrom and Johan Ugander called balanced label propagation. In order to make it faster on our largest datasets, we adapted it to fit Giraph’s model of distributed computing.
Each Giraph worker (a machine in the cluster) holds part of the graph. The partition a vertex currently belongs to is an attribute of the vertex. Initial assignments can be either specified by the engineer or drawn at random.
At the beginning of an iteration, each vertex communicates its current partition to its neighbors by sending messages. Then, based on the incoming messages, each vertex can compute how many of its neighbors are currently assigned to each partition. If a partition contains many more neighbors than the current one, the vertex may choose to relocate (see Figure 3). Instead of simply selecting the partition with the highest number of neighbors, we choose it probabilistically with a bias toward higher counts. This prevents the algorithm from getting stuck when the constraints don’t allow a certain move.
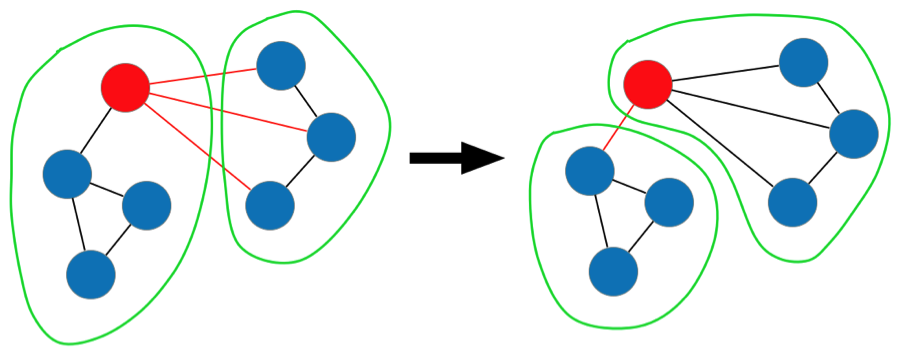
Figure 3: Example of a move that increases local edges
Once a vertex has chosen its candidate partition, we don’t immediately reassign it – by doing so, we could produce an imbalance in the partition sizes. Instead, the vertex signals that it wants to move from partition i to partition j, and these counts are aggregated globally for each pair of partitions. A master computation then determines how many vertices can actually be moved between two partitions so that balance is maintained: If m_ij is the total number of candidates for moving from i to j, we allow to move x_ij = min(m_ij, m_ji) vertices. (Linear programming could also be used here, but we found this simple method to be more scalable and almost as effective.) This information is then propagated to the workers.
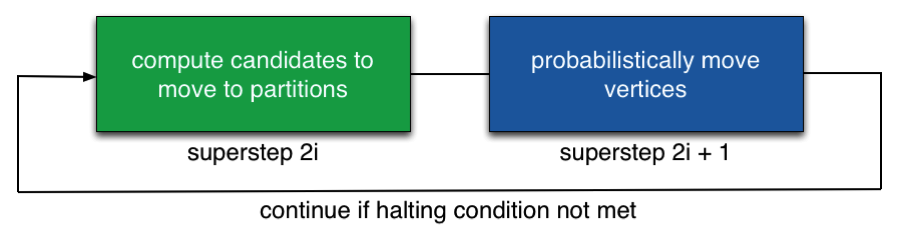
Finally, for each partition pair, the required number of vertices are relocated. In order to accomplish this in parallel, we use the following procedure: For each vertex that wants to move from i to j, we toss a biased coin with probability x_ij/m_ij. If the outcome is positive, the vertex is assigned to partition j; otherwise, it remains in partition i. For large enough datasets, this achieves nearly perfect balance in practice. The algorithm then terminates when the percentage of local edges stabilizes, or when a maximum number of iterations is reached.
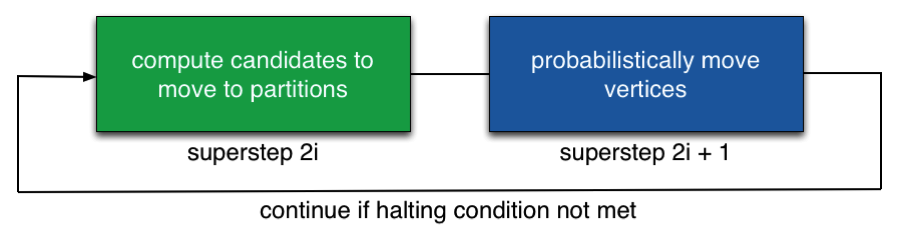
Figure 4: Each iteration of the algorithm consists of two supersteps in the BSP model
In order to obtain a better starting point, we exploited a well-known feature of the social graph: Facebook users tend to be friends with people who live nearby. By initializing the algorithm with partitions based on geographical proximity, the algorithm achieves better results in shorter time, as we show in the next section.
A useful property of this algorithm is that, as new users join and form new connections, we can incrementally update the partitioning with minimum effort – we simply initialize the algorithm with the previous partitions (e.g., computed the day before) and run it on the new version of the graph. Within a couple of iterations (typically one suffices), the original edge locality is restored.
In addition to the model above, our implementation also supports graphs with weighted vertices and edges: if non-uniform vertex weights are specified, the algorithm balances partitions in terms of total weight (instead of number of vertices). If edge weights are specified, the total weight of local edges is maximized (as opposed to the total number of local edges). These generalizations are useful for certain applications, where some people on Facebook are more active than others or some friendship edges are queried more often. The following analysis deals with the unweighted case.
Results
We ran the algorithm above on the graph of Facebook monthly active users, which comprised more than 1.15 billion people and 150 billion friendships at the time of the experiment (this corresponds to 300 billion edges, since Giraph’s model is based on directed graphs). We used 200 machines from our cluster for the computation. Both random and geographic initialization were tested for dividing the graph in 100 partitions.
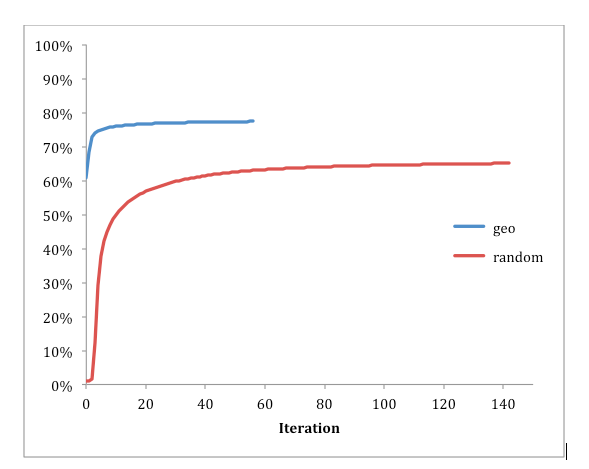
Figure 5: Edge locality across iterations
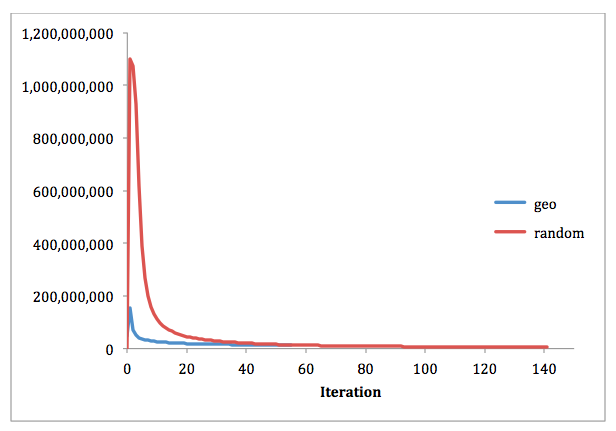
Figure 6: Vertices relocated in each iteration
Loading the graph took about five minutes (six minutes when also loading initial partitions). Each iteration of the algorithm took under four minutes. With random initialization, the percentage of local edges went from 1% to 65% in 137 iterations. When initialized using geographical information, the starting point was 60.8% local edges, which our algorithm improved to 76% in just 10 iterations and 77% within 31 iterations.
To see the impact of such an improvement on a distributed system, we used Giraph to run the PageRank algorithm on the same graph, this time utilizing 100 machines. At the beginning of each Giraph job, the graph is loaded from a distributed file system and partitioned across workers. With standard, hash-based partitioning, virtually all edges span different workers. In order to easily exploit our improved partitioning, we numbered all vertices in order of partition, and used Giraph’s range partitioner. With the default hash-based strategy, an iteration took 363 seconds on average. When using our special partitioning, iteration time was down to 165 seconds–over twice as fast.
An early adopter within the company was a service in which typical queries involve fetching a considerable amount of data for each of a person’s friends. The service employs a caching layer to keep the most recent results in memory. The caching layer is divided in shards, such that each person is consistently directed to the same shard. By identifying each shard with a graph partition, a person will likely be co-located with most of his or her friends. This helped increase the hit rate and reduce data duplication across machines, and the end result was a 2x improvement in bandwidth utilization.
Graphs are widespread at Facebook, and many systems can benefit from an intelligent layout of the data. We are already working on new heuristics to achieve even better edge locality.
This work was carried out by software engineers Alessandro Presta, Alon Shalita, Brian Karrer, Arun Sharma and Igor Kabiljo; along with former interns Aaron Adcock and Herald Kllapi.